Gas EOR Processes in Tight Unconventionals

Author: Stian Mydland

*This is a short-version of SPE-200396-MS to be presented at SPE Increased Oil Recovery Conference 2020, Tulsa, OK, USA.

Gas-Based EOR in Tight Unconventionals

Gas-based EOR is currently being pilot-tested extensively in liquid-rich North-American tight unconventionals with the majority of projects using the Huff-n-Puff (HnP) method. This method differs from conventional displacement EOR because it uses a single well for both injection and production. HnP is not a displacement-type EOR method, but rather a method that achieves enhanced oil recovery by mixing of injection gas and oil near the wellbore/hydraulic fractures. The greater degree of mixing in a HnP process, the higher the expected oil recovery.

Because the HnP method is a mixing-based EOR method, the conventional multi-contact miscibility theory for gas displacement processes is less relevant. Carlsen et al. (2019) argued that the performance of HnP is largely controlled by the first-contact minimum miscibility pressure (MMP_FC) and its relation to the HnP operating pressures (i.e. the minimum and maximum pressure during each cycle). The term (p_inj – p_sat)/(p_inj – p_wf) reflects the HnP recovery efficiency when complete mixing is assumed. A value ≥1 for a given injection period indicates a swelling process (single-phase) where the quantity of reservoir oil that fully mixes with injection gas during the injection period (into a single-phase mixture) is completely recovered during the production period. A value between 0 and 1 indicates a combination of recovery by swelling and vaporization, and a value of ≤0 indicates recovery by vaporization only (two-phase). HnP is most efficient when the method is a swelling process (single-phase, (p_inj – p_sat)/(p_inj – p_wf)≥1), and least efficient when it is a vaporization process (two-phase, (p_inj – p_sat)/(p_inj – p_wf)≤0).

Modeling the Huff-n-Puff Method

Reservoir modeling of HnP is important for decision-making. However, reservoir modeling of the HnP EOR process requires different considerations compared with modeling of primary pressure depletion. If we consider the simplest model of a hydraulic fracture draining a slab of low-permeability rock – the so-called planar-fracture model – the expected physical recovery process would consist of gas miscibly displacing oil away from the well during the huff period, and the injection gas being produced back during the puff period, i.e. a process that yields no enhanced oil recovery. The process behaves essentially as a piston, with gas pushing the piston and the piston pushing the oil out in the reservoir.

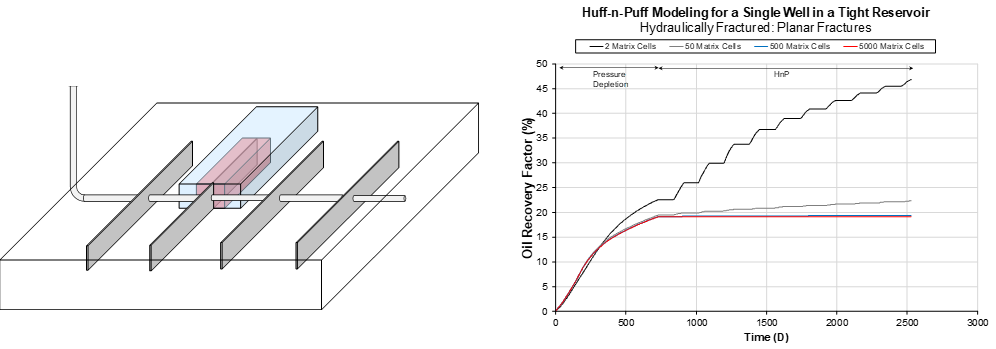
If the numerical gridding of this process is sufficient, then a converged solution with near-zero incremental recovery results. However, if grid sizes are too large and the gridding is insufficient to capture the sustained miscible displacement away from the well, artificial mixing of the injection gas and reservoir oil results in excessive incremental oil recovery. The coarser the grid, the higher the false incremental recovery. This grid sensitivity applies to the blue region in Fig. 1 (left).

Observed incremental recovery of the HnP processes in field tests must result from some other mechanism. We believe that around the hydraulic fracture, there is a region of shattering that consist of small pieces of rubble (debris). This is represented by the red region in Fig. 1 (left). This shattered volume (SV) is a dual-porosity system whereby injected gas surrounds the rubble at high pressure, and mixes with the oil in the rubble through a process driven mostly by molecular diffusion and large cyclic pressure changes.   

A simple single-fracture, symmetry-element model can be used to achieve the necessary grid refinement for HnP. A sketch showing such a model is given in Fig. 1 (left). The blue region represents the reservoir model, the red region represents the shattered volume, and the gray planes represent the hydraulic fractures. Fig. 1 (right)shows the effect of grid blocks on the HnP incremental recovery for the case where an SV does not exist. The results behave as already stated; incremental recovery approaches zero with increasing number of grid blocks.

The SV [i.e. the red region in Fig. 1 (left)] is included in the model by using a dual-porosity (DP) treatment. However, this requires that the HnP performance from the DP model is tuned to reflect the physical HnP performance that can only be modeled consistently with a detailed single-porosity (SP) treatment where diffusion is included [along the lines off Coats (1989)]. This performance check is done by modeling the recovery from a single set of DP grid blocks (one matrix grid block and one fracture grid block), and then compare this recovery to the recovery predicted by a single matrix block in the SV that is modeled by a SP treatment with diffusion. Fig. 2 shows the set of DP grid blocks, and how the SP treatment is used to model the performance of a single matrix block (“sugar cube”) in the Warren–Root block.

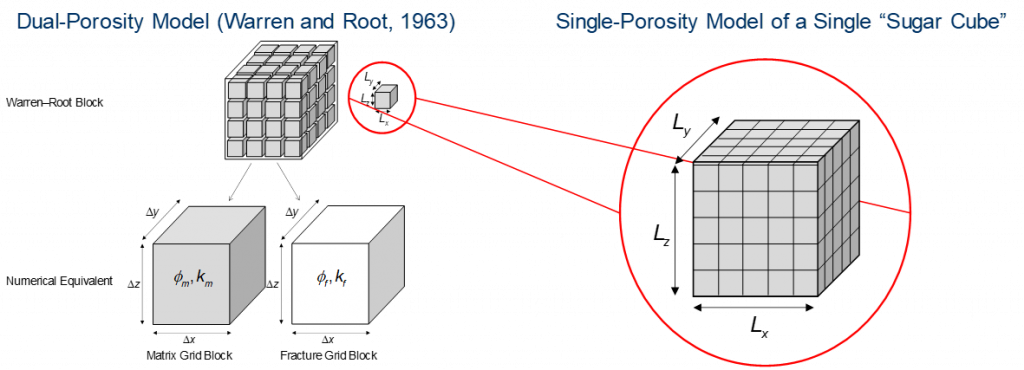
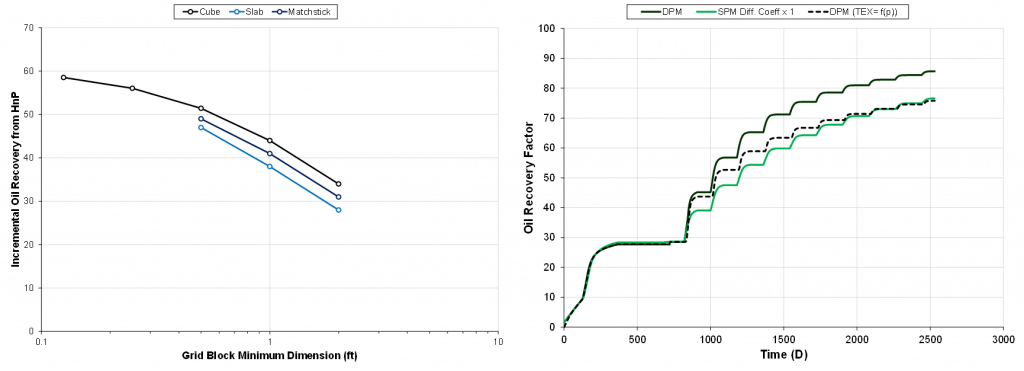
Fig. 3 (left) shows the incremental recovery for cubes, slabs, and matchsticks, as a function of the smallest dimension for the SP model with diffusion. The results indicate that the incremental recovery is mostly a function of this minimum dimension, and less sensitive to the geometry itself (or surface area). Fig. 3 (right) shows the HnP recovery profile from modeling a 1x1x1 ft³ matrix block using a SP model with diffusion and set of DP grid blocks. Tuning of the DP model is needed to match the recovery predicted by the SP model, and this was achieved by introducing a pressure dependence on the matrix-fracture exchange transmissibility.

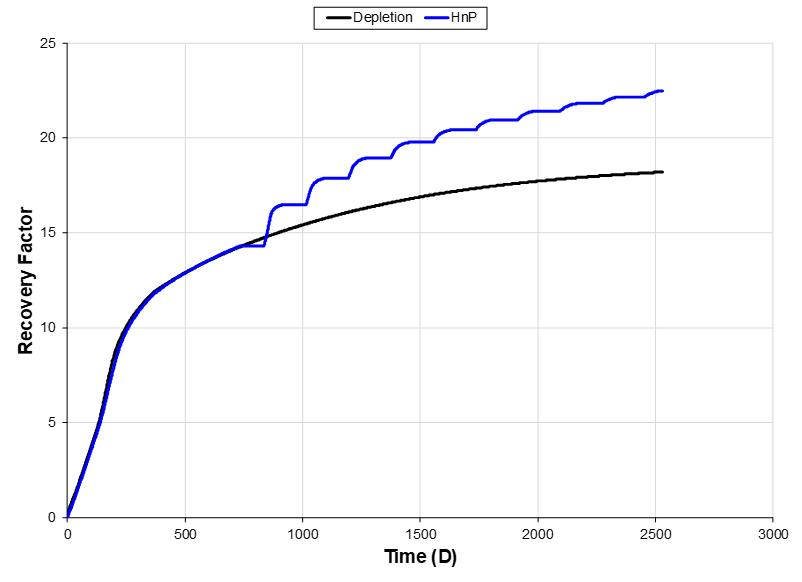
The tuned set of DP grid blocks are then used to populate the SV part of the symmetry-element model in Fig. 1 (left) (i.e. the red region). Fig. 4 shows the recovery factor for HnP compared to recovery factor for pressure depletion. We see that applying HnP after 2 years of depletion results in an incremental recovery of ~5% after ten 180-day HnP cycles.

Summary

1. Modeling of gas-based EOR requires a large number of grid blocks in the unfractured region (matrix only) to eliminate numerical dispersion.
2. The shattered volume is a premise for incremental recovery from HnP.
3. The dual-porosity model can be used to provide a good representation of the SV recovery process by HnP. This requires, however, that the dual-porosity model is tuned to the performance of a single-porosity model where diffusion is included.

Learn more about our consulting capabilities

###

Global
Curtis Hays Whitson
curtishays@whitson.com

Asia-Pacific
Kameshwar Singh
singh@whitson.com

Middle East
Ahmad Alavian
alavian@whitson.com

Americas
Mathias Lia Carlsen
carlsen@whitson.com

About whitson
whitson supports energy companies, oil services companies, investors and government organizations with expertise and expansive analysis within PVT, gas condensate reservoirs and gas-based EOR. Our coverage ranges from R&D based industry studies to detailed due diligence, transaction or court case projects. We help our clients find the best possible answers to complex questions and assist them in the successful decision-making on technical challenges. We do this through a continuous, transparent dialog with our clients – before, during and after our engagement. The company was founded by Dr. Curtis Hays Whitson in 1988 and is a Norwegian corporation located in Trondheim, Norway, with local presence in USA, Middle East, India and Indonesia