Author: Sissel Martinsen
In our monthly article “How to Quality Check a Developed EOS” we addressed methods to check that an EOS model calculates physically consistent properties and thermodynamic valid solutions. A thermodynamic consistent EOS model is a model that gives consistent phase behavior of mixtures, and individual components.
Part of our standard EOS QC is that K-values don’t “cross” for most hydrocarbons. Crossing K-values would suggest that neighboring components (usually ordered by increasing normal boiling point) change their relative preference to partition into the gas and oil phases as a function of pressure. Such crossing-K-value behavior can exist for some isomers of a given/similar carbon number, but crossing K-values are not expected for single carbon numbers (SCN). We certainly don’t expect the very heaviest component (e.g. C36+) to have a K-value greater than the heaviest SCN (e.g. C35) at any pressure.
As a part of the physical consistency of the EOS we suggested making the following plots:
- Normal boiling point, Tbi, versus carbon number or molecular weight (Mi) for C6+ components
- Critical temperature and pressure versus Tbi or Mi
- Liquid density at standard conditions versus Mi or Tbi for C6+ components
- Liquid viscosity versus Mi or Tbi for C6+ components
Critical properties (Tci, pci, ωi) of the C7+ components and binary interaction parameters (BIPs) of an EOS are often tuned to improve the phase behavior predictions of lab PVT data. It is easy to assume if all hydrocarbon-hydrocarbon BIPs are smooth and consistent and if all the physical consistency plots show monotonic behaving Tb, Tc, pc versus SCN, that the EOS will not exhibit crossing K-values for SCNs.
Sometimes, however, this is not the case. In this monthly article we show a few examples where the critical properties of the C7+ characterization are all monotonic changing with increasing carbon number, but the EOS still results in crossing K-values.
EOS tuning usually tunes (adjusts) component properties and BIPs that (1) give high impact on phase behavior predictions with small change in value, and (2) have some uncertainty.
The critical properties of the heaviest component are often used as regression variables because we do not know values with any certainty. This article studies specifically the impact of tuning the heaviest component properties.
We use the SRK EOS model with all BIPs set to 0. The composition contains only hydrocarbons and is given in Table 1.
The C7+ fraction is split in single carbon numbers from C7 to C35 with C36+ as the heaviest component using an exponential distribution with an average molecular weight of 220 g/mol.
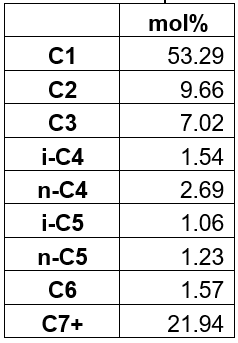
In Fig.1 the saturation prediction dependency on critical properties of C36+ is given. A single multiplication factor was applied to one of the default C36+ properties (Tb, Tc, or pc). For this article, the Tb was modified [1] in a way that only changes the acentric factor (w) of C36+. Mixture saturation pressure is calculated at 178 oF. From Fig. 1 we see that a small change in critical temperature or normal boiling point (i.e. acentric factor) of C36+ gives a significant change in predicted saturation pressure.
The change in boiling point shown here is equivalent to changing only the acentric factor, without any change in critical pressure or temperature. The normal tuning practice used at whitson for modifying boiling point is different, where the critical pressure, critical temperature, and acentric factor are all modified when boiling point is modified – i.e. a “consistent” property change due to the uncertainty in normal boiling point of petroleum fractions.
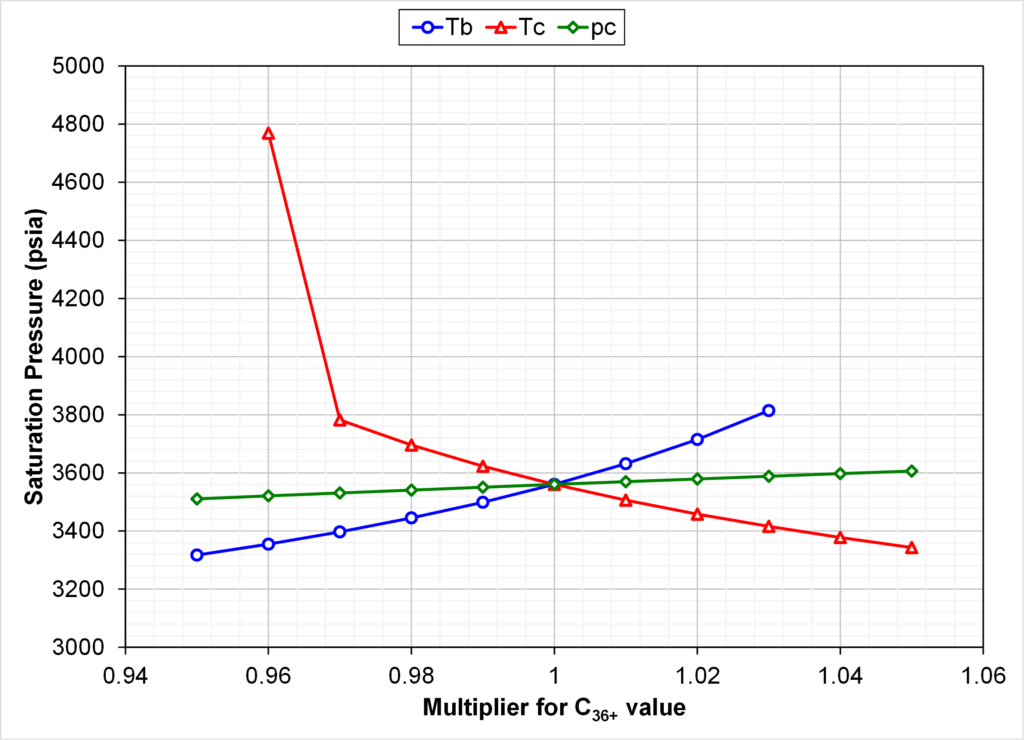
Fig. 2 shows that increasing the critical temperature of C36+ by only 2% leads to undesired crossing K-values (C35 and C36+ K-values are equal). This figure shows K-value of C35 and C36+ at a pressure of 3250 psia for varying C36+ critical temperatures. All other properties of the EOS models are identical.
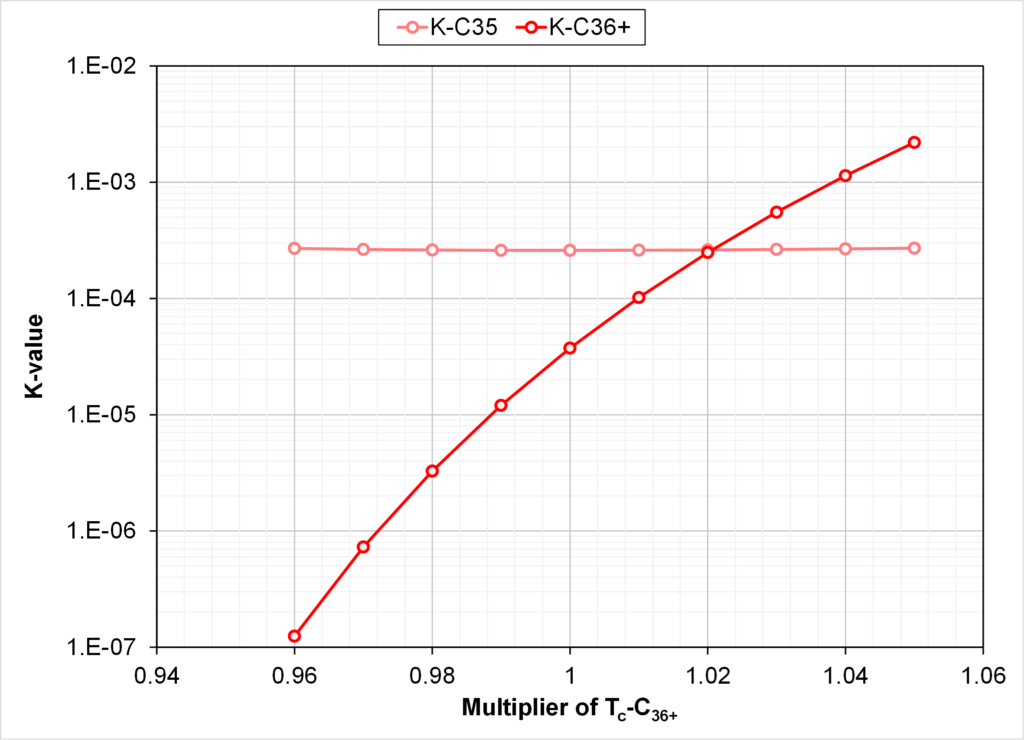
The critical properties of the C7+ fraction in the default EOS are shown in Fig. 3. An EOS with multiplication factor 1.03 for Tc of C36+ is shown in the same figure.
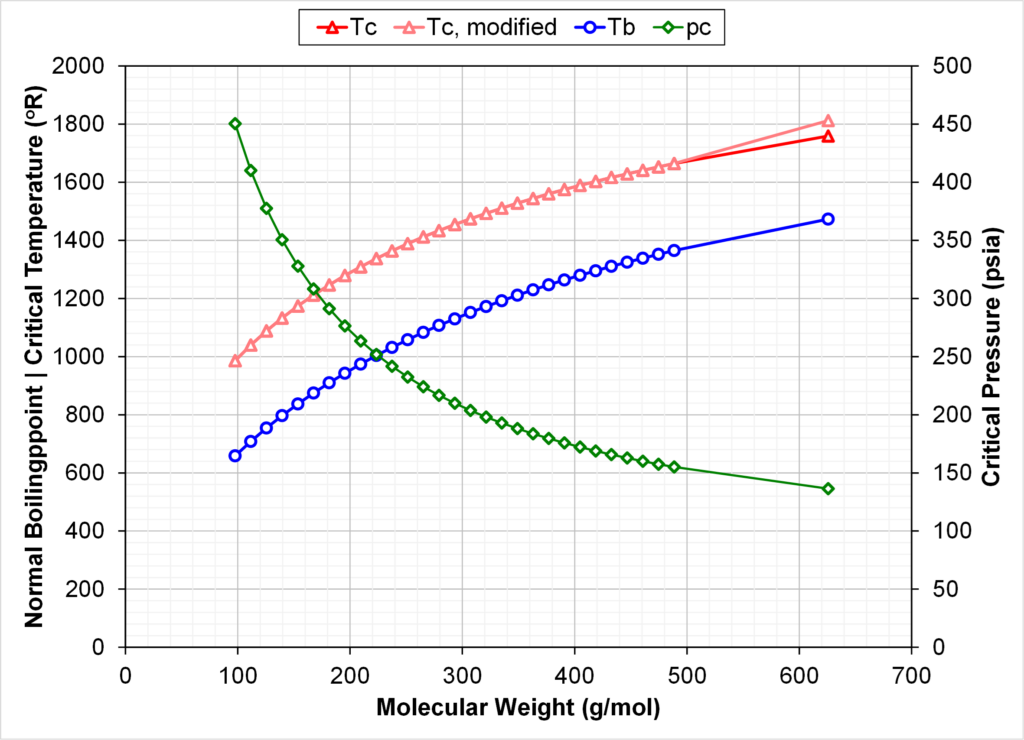
Fig. 4 compares the calculated K-values at 3250 psia and 178 oF using two EOS models: (1) default SRK EOS model with all zero BIPs and (2) an identical EOS model but with Tc of C36+ being 3% higher than the default EOS.
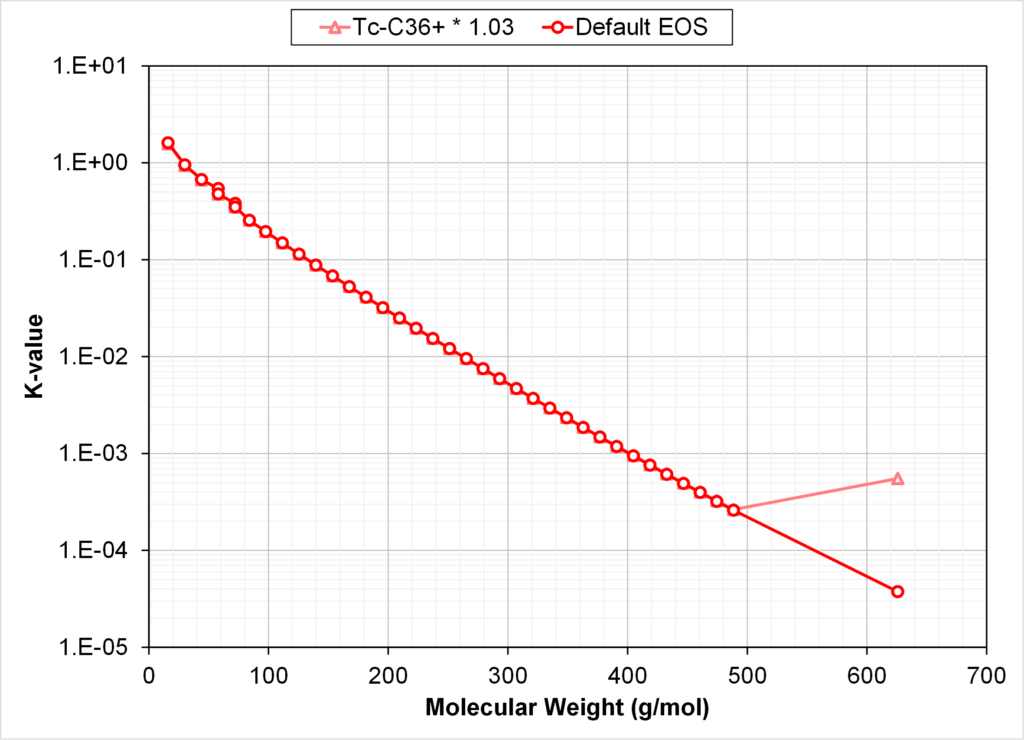
From Figs. 3 and 4 we see that increasing the Tc of C36+ by 3% gives monotonic Tc’s versus Mi & Tb,i, but with C36+ K-values that are higher than the K-value of C32.
Modifying the normal boiling point temperature of C36+ by updating the acentric factor may also result in crossing K-values. Fig. 5 show that crossing K-values are more likely when regressing on C36+ Tb than on C36+ pc. This figure gives the K-values of C35 and C36+ at a pressure of 3250 psia for varying pc and Tb of C36+. All other properties of the EOS models are identical.
As mentioned in footnote 1, our normal procedure for using boiling point as a regression variable will change in a consistent way the three component properties (Tc, pc, w). When making this consistent alteration of boiling point for C36+, we find that a decrease of almost 9% is required in Tb to cause crossing K-values between C35 and C36+.
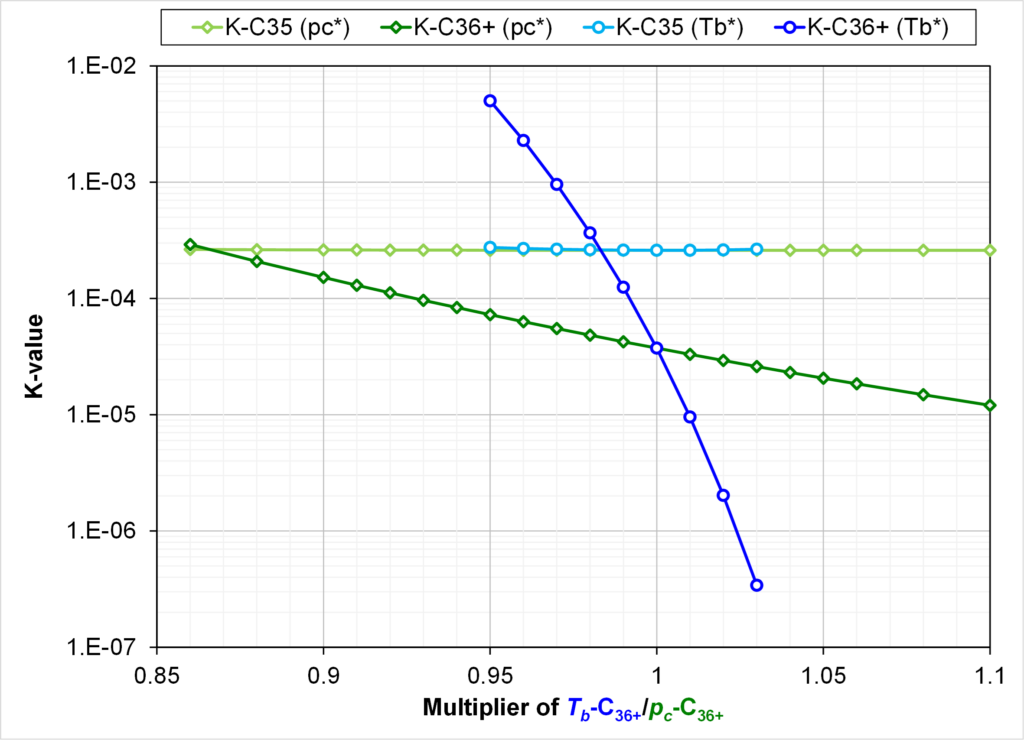
Fig. 5 shows that decreasing the normal boiling point of C36+ by only 2% gives crossing K-values. A decrease in Tb of C36+ by 2% still gives smooth monotonic Tb,i versus Mi.
So, why can an EOS with zero BIPs and monotonic behaving critical properties give crossing K-values? Michelsen showed that K-values can be calculated exactly with the following equation for all zero BIPs:
| $$\log{(K_i)}=C_0+C_1\sqrt{a_i}+C_2b_i$$ | (1) |
where
| $$a_i=\Omega_a^0\frac{R^2T_c^2}{p_c}\alpha_i$$ | (2) |
| $$ b_i=\Omega_b^0\frac{RT_c}{p_c} $$ | (3) |
and the three constants C0, C1, and C2 are known from the EOS flash calculation at a specific (p,T) and composition. Crossing K-values of neighboring components Km and Kn exist when Km=Kn. This condition arises when
| $$\frac{\sqrt{a_m}-\sqrt{a_n}}{b_n-b_m}=\frac{C_2}{C_1}$$ | (4) |
Summary
So, in conclusion, to ensure a thermodynamically consistent EOS model it is important to check that the critical properties of the EOS model are monotonic, but also to check for monotonic K-value behavior of hydrocarbon fractions at relevant pressures and temperatures.
Note:
[1] The change in boiling point shown here is equivalent to changing only the acentric factor, without any change in critical pressure or temperature. The normal tuning practice used at whitson for modifying boiling point is different, where the critical pressure, critical temperature, and acentric factor are all modified when boiling point is modified – i.e. a “consistent” property change due to the uncertainty in normal boiling point of petroleum fractions.
###
Le Learn more about our software products
Global
Curtis Hays Whitson
curtishays@whitson.com
Asia-Pacific
Kameshwar Singh
singh@whitson.com
Middle East
Ahmad Alavian
alavian@whitson.com
Americas
Mathias Lia Carlsen
carlsen@whitson.com
About whitson
whitson supports energy companies, oil services companies, investors and government organizations with expertise and expansive analysis within PVT, gas condensate reservoirs and gas-based EOR. Our coverage ranges from R&D based industry studies to detailed due diligence, transaction or court case projects. We help our clients find the best possible answers to complex questions and assist them in the successful decision-making on technical challenges. We do this through a continuous, transparent dialog with our clients – before, during and after our engagement. The company was founded by Dr. Curtis Hays Whitson in 1988 and is a Norwegian corporation located in Trondheim, Norway, with local presence in USA, Middle East, India and Indonesia
