Author: Arnaud Hoffmann
To reduce CPU time in compositional petroleum simulation models (e.g. compositional reservoir simulations), a minimum number of components should be used in the equation of state (EOS) to describe the fluid phase and volumetric behavior. A ″detailed” EOS model often contains from 20 to 40 components, with the first 10 components representing pure compounds (H2S , CO2, N2, C1, C2, C3, i-C4, n-C4, i-C5, and n-C5) and the remaining components representing a split of the heavier C6+ material in single-carbon-number (SCN) fractions. A ″pseudoized” (or lumped) EOS model might contain only 6–9 lumped components. Occasionally the light aromatics BTX (benzene, toluene, and xylene isomers) are also kept as separate components for
process modeling. Today’s typical laboratory compositional analysis provides 50–60 components, including isomers with carbon numbers 6 to 10, SCN fractions out to C35 and a residual C36+.
The selection of which components to lump together is difficult because of the huge number of possible combinations. Let us assume that a detailed SCN EOS model, EOSxx, consisting of \(N_{xx}\) components is available and represents with a satisfying degree of accuracy the measured lab data. For some reasons, a lumped EOS, EOSx, is required with \(N_x\) components. Creating a lumped EOS with \(N_x\) components from a detailed EOS with \(N_{xx}\) components consists of choosing where to place \(N_x – 1\) separators in the \(N_{xx} – 1\) possible separation locations, see Figs. 1 and 2.
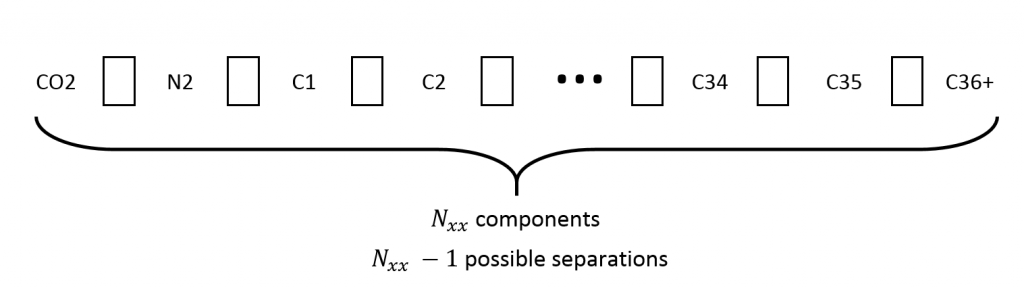
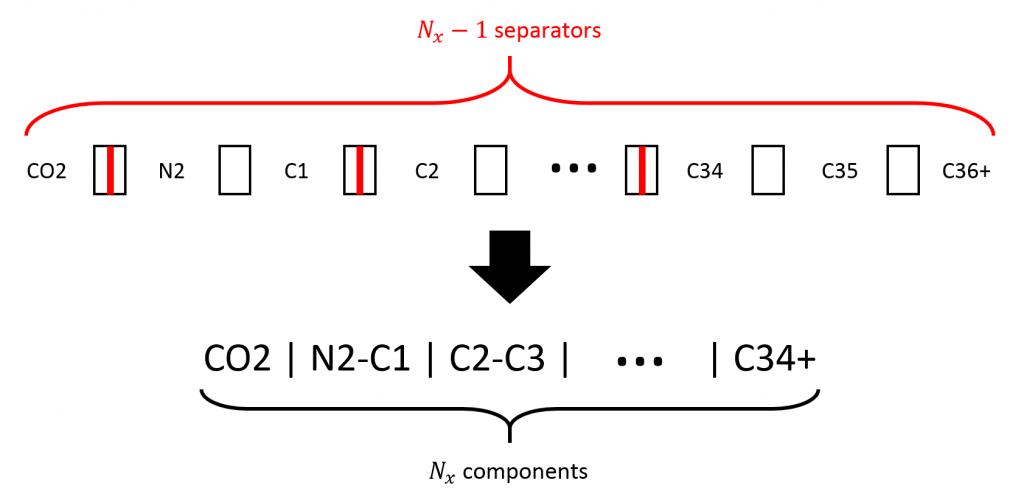
Thus, the number of possible lumping scenarios \(N_{scenarios}\) is given by:
$$N_{\mathrm{scenarios}} = \dbinom{N_{xx} – 1}{N_x – 1} = \frac{(N_{xx} -1)!}{(N_x-1)!(N_{xx} – N_x)!}.$$
For example, with \(N_{xx} =34\)and \(N_{x} = 9\) there are \(N_{scenarios} = 13,884,156 \) possible lumping schemes.
On the one hand, lumped EOS enables to lower considerably the runtime of some discipline specific applications (e.g. reservoir simulator). On the other hand, the lumping scheme can have major impact on the accuracy of the EOS predictions, see Fig. 3. This is why finding the optimal EOS lumping scheme is important. For the same number of pseudo-components (i.e. the same runtime in engineering software applications), fluid behavior predictions can be significantly different, see Fig. 3.
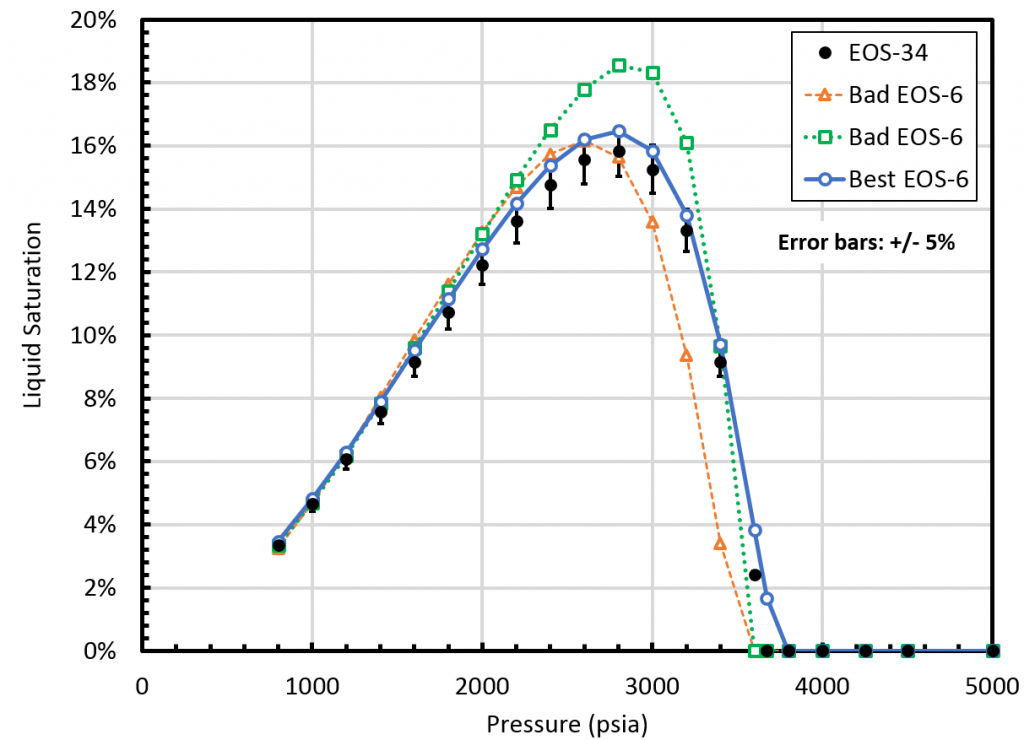
EOS component lumping is a topic that is extensively covered in the litterature:
- Lee et al. (1982) suggest that \(\mathrm{C}_{7+}\) fractions can be grouped into two pseudo-components according to a characterization factor determined by averaging the tangents of fraction properties molecular weight, specific gravity, and Jacoby factor plotted vs. boiling point.
- Whitson (1983) suggests a method to estimate the number of \(\mathrm{C}_{7+}\) fractions, and how they should be grouped.
- Coats (1985) discusses in detail lumping of \(\mathrm{C}_{7+}\) fractions for modeling the vaporization process in gas condensate cycling. He gives a set of fundamental criteria and methods to calculate the EOS parameters of lumped pseudo-components. The impact of lumping on PVT model quality and reservoir simulation modeling of a gas cycling process is also shown.
- Behrens and Sandler (1988) suggest a grouping method for \(\mathrm{C}_{7+}\) fractions based on application of the Gaussian-quadrature method used in continuous thermodynamics.
- Whitson et al. (1989) show that any \(\mathrm{C_{7+}}\) molar-distribution can be modeled with the Gamma distribution with any number of pseudo-components.
- Other pseudoization methods have been proposed by Montel and Gouel (1984), Li et al. (1985), Newley and Merrill (1991), Danesh et al. (1992) and Hustad and Dalen (1993).
However, none of them ensures the selection of the optimal lumping scheme. Alavian et al. (2014) were the first to present a method with the guarantee to find the optimal pseudoized EOS model to describe all PVT data that is relevant to a particular reservoir development (e.g. depletion performance, miscible gas injection, compositional variation, surface processing). The method tests all possible lumping scenarios and assesses the quality of individual scenarios by quantifying its mismatch from the detailed EOS model using a root mean square (RMS) error. The method always finds the best lumping scheme but the runtime can be significant because it tests every single possible lumping scenario.
Hoffmann (2019) presents an optimization technique consisting of (1) a genetic algorithm used to get a good set of “good” starting points that are (2) refined using a tabu algorithm. The proposed method was tested on all cases of Alavian et al. (2014) and was able to find the optimal lumping schemes with a runtime ranging from 10 to 50 minutes.
Application
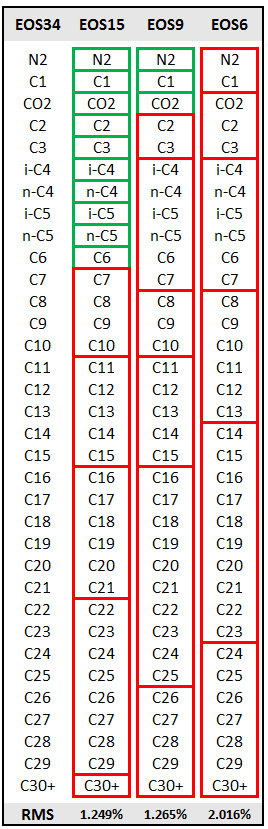
Alavian et al. (2014) consider an EOS model with 34 components describing with a desired degree of accuracy some 1200 PVT measurements. They apply their method to three cases:
- Lumping EOS-34 into EOS-15 (10 light components fixed)
- Lumping EOS-34 into EOS-9 (3 light components fixed)
- Lumping EOS-34 into EOS-6 (no component fixed)
Conclusions
There are many method available for lumping EOS models, but most of the methods do not guarantee that the selected lumped EOS is the optimal for preserving the quality of the phase behavior predictions. Finding the optimal lumping schemes when lumping components from a detailed EOS model to a simplified EOS model is crucial to maintain a good representation of reservoir fluid behavior. There is no simple and intuitive way to carry out that operation. To our knowledge there are only two solutions available that will always guarantee finding the optimal lumped EOS model:
- A global search that evaluates every possible lumping scheme and select the best(s) schemes. This search is presented in Alavian et al. (2014).
- Using integer optimization techniques to minimize the number of model evaluations (and thereby reduce the runtime) without jeopardizing the quality of the solutions. This is the approach presented by Hoffmann (2019).
whitson engineers have been successfully using both approaches on numerous projects over the last years.
References
[1] Hoffmann, A., EOS lumping optimization using a genetic algorithm and a tabu search, 2019. Journal of Petroleum Science and Engineering, 174, p. 495-513.
[2] Alavian, S.A., Whitson, C.H., Martinsen, S., 2014. Global component lumping for EOS calculations. In: Presented at the SPE Annual Technical Conference and Exhibition, 27-29 October. Society of Petroleum Engineers, Amsterdam, The Netherlands. https://doi.org/10.2118/170912-MS.
Learn more about our consulting capabilities
###
Global
Curtis Hays Whitson
curtishays@whitson.com
Asia-Pacific
Kameshwar Singh
singh@whitson.com
Middle East
Ahmad Alavian
alavian@whitson.com
Americas
Mathias Lia Carlsen
carlsen@whitson.com
About whitson
whitson supports energy companies, oil services companies, investors and government organizations with expertise and expansive analysis within PVT, gas condensate reservoirs and gas-based EOR. Our coverage ranges from R&D based industry studies to detailed due diligence, transaction or court case projects. We help our clients find the best possible answers to complex questions and assist them in the successful decision-making on technical challenges. We do this through a continuous, transparent dialog with our clients – before, during and after our engagement. The company was founded by Dr. Curtis Hays Whitson in 1988 and is a Norwegian corporation located in Trondheim, Norway, with local presence in USA, Middle East, India and Indonesia
